3333333333333333333 but beaten badly
The commitment curve is vertical
Two extremes
Factory games are mainly about answering the question of: "With these bits and pieces, how efficiently can I fulfill this objective?"
Efficiency here is most often defined in terms of space or time, but other metrics are also possible. Opus Magnum, for instance, asks you to optimize for the machine's cost.
There is a dual to this question that, once you hit a certain threshold of control over the bits and pieces you're given, becomes trivial. That is to say, more often than not, the answer to "With these bits and pieces, how inefficiently can I fulfill this objective?" is infinite. (Precisely, only limited by the player's patience in scheduling moves that cancel each other out, yielding a time of omega.)
But, when you don't have that level of control, more often than not, this is a genuinely interesting question to ask. For instance, in a tiny 5x5x1 footprint, a redstone signal in Minecraft can be delayed for a nonsensical 48 years.
You know what else is fun about deoptimizing? Breakthroughs don't shave 0.3 points off your score, they add 100,000,000. Big numbers are funny.
3333333333333333333
3333333333333333333 is a factory game where the objective is to use arithmetic operations to output 33 .
The player can change the initial positions of the numbers and arithmetic symbols, which we'll call "components" from now on. It's also possible to place belts, which, once the machine is started, shift the numbers and symbols on top of them to the tile ahead every cycle. The "del", where extraneous digits may be dumped, and the "out 9", where the 33 must be routed to, can also be moved. We'll call these two special tiles "sinks" from here on out.

This solution by Kinwoods completes in 82 cycles.
The most efficient record at the time or writing is a setup of 16 belts that completes 33333333333333333333 (henceforth 19x3) in only 34 cycles.
But of course, that's not the question we're here to ask.
So. How badly can we do?
One loop
The first thing we need to establish is what calculations exactly we want our machine to perform. The smallest calculation loop that outputs a is as follows:
- Store one of the
- Output one . Retrieve the stored
- Loop from step 2
19x3 is nineteen squares wide and fourteen squares tall. That's 266 tiles of space to work with. The smallest calculation loop can be set up with only 22 tiles of space, which produces a on cycle 2 and then every 5 cycles after that, since 5 is the length of the lower track.

The equals sign can be on the left, too.
This solution leaves 244 tiles of space with which we can extend the lower track to 249 belts. As a result, with one circuit, we can build a machine that completes in 2 + 32(249) = 7970 cycles.
Can we do worse?
Yes, actually. That "24 tiles of space" number from earlier includes the three tiles that three of the move into to get into position to form . But because of how each step processes computations first and movements after, two of these tiles can contain belts. The will be moved onto the belts, but get multiplied away before the belts can move them in the next cycle. As a result, with one circuit, we can build a machine that completes in 2 + 32(251) = 8034 cycles.


Just give it three or four minutes. It'll get there. Trust.
Can we do worse?
Yes, actually. After all, our machine is currently doing two computations. If we could draw an extremely long loop that cut through both of them in such a way that both computations took upwards of 200 steps to complete, we would have a machine that completes in upwards of 12,000 cycles.


The belts are set up so that the number stays behind the equals sign. You can check for yourself that, with this bend of the belt in the center, the two computations require this.
Can we do worse?
Yes, actually. By using a belt to move the first onto the giant loop (or by directly routing the giant loop through the tile where it's created) and placing the output sink just before this point in the loop, we can force the created to travel almost the entirety of the loop in the wrong direction before being outputted.
Add to that a small change in the shape of the loop to reduce the number of belts needed on the bottom and left, and we score a very respectable 16615.
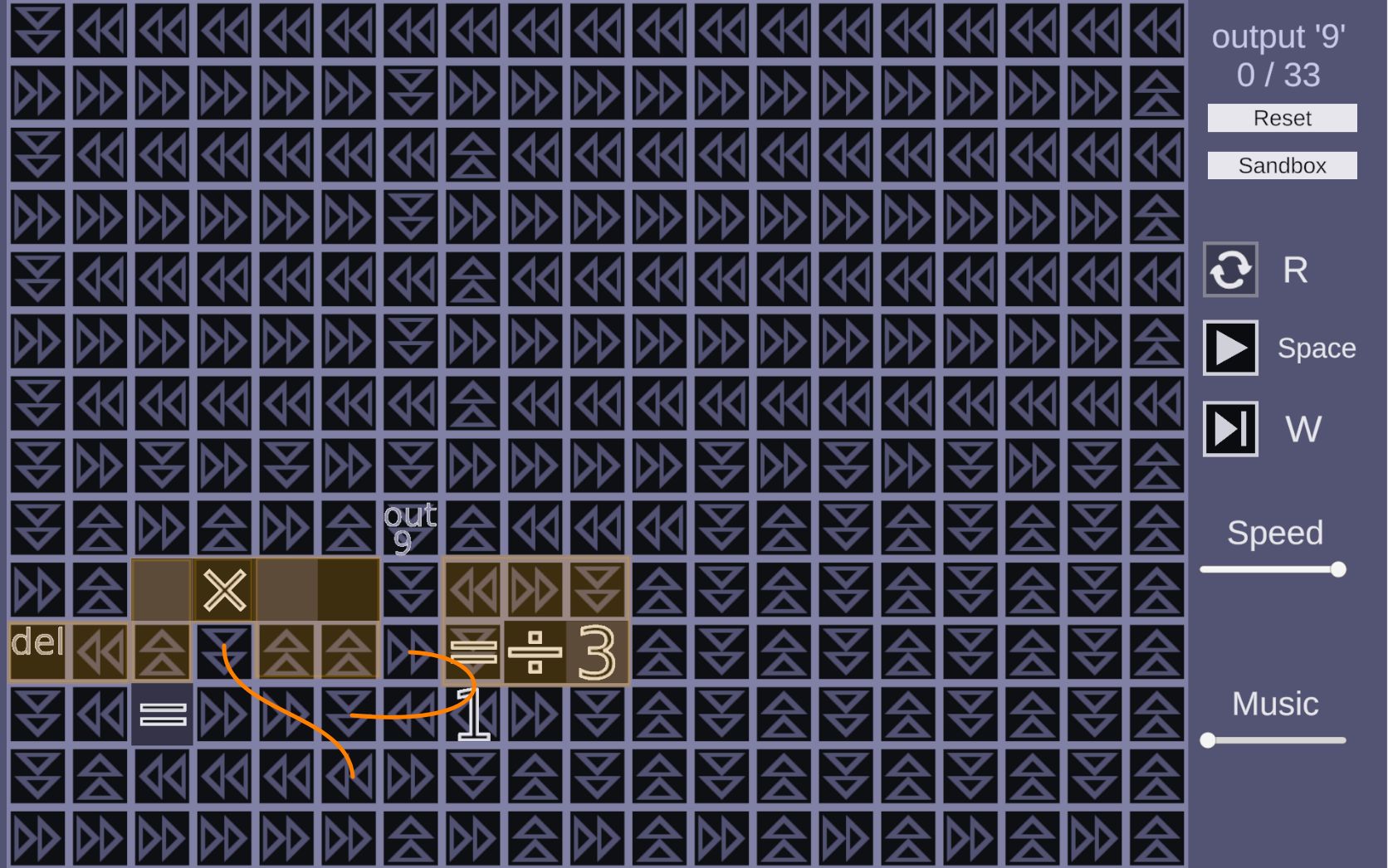

I'm leaving these machines running in the background while I write this post.
Not bad, for only being allowed one loop.
Multiple loops
When it comes to simple moving parts like the belts of factory games, one of the biggest possibilities for shenanigans is the Chinese Remainder Theorem.
Basically, if are pairwise coprime, objects looping on belts of lengths will cycle through every possible combination of offsets before finally lining up once every cycles.
In other words, if we can set up a machine that has to wait for the alignment of things in a space of tiles, it will end up being .
Here's a prototype for a machine with four loops.

We're now creating 5 to make routing the loops easier. As a result, the is travelling over the "del" sink, since we need to get rid of an unnecessary . Thus, the bin is moved onto the loop, and the and are routed to the bin instead of being spawned directly on top of it. We've also switched from computing to to expose the bin.
What configuration of four belts yields the least efficient machine?
Let's suppose that the occurs steps after the assembles, meaning that the and move steps before the appear behind them. This forms an optimization problem:
The 257 is gotten by subtracting from the available 266 tiles of space 2 symbols (), 2 holding spots (the of and the leading of ), and 5 belts that move numerals into holding spots.
Here's a quick and dirty Python script assembled to solve this optimization:
from math import floor, gcd, sqrt
from typing import Generator, Any
from tqdm import tqdm # type: ignore
def crt(a1: int, m1: int, a2: int, m2: int):
"""
Solve the system:
x ≡ a1 (mod m1)
x ≡ a2 (mod m2)
Returns (x0, M) where x ≡ x0 (mod M) for all solutions, with 0 ≤ x0 < M.
Returns (None, None) if there is no solution.
"""
g = gcd(m1, m2)
if (a2 - a1) % g != 0:
return None, None
m1_reduced = m1 // g
m2_reduced = m2 // g
# Solve: m1 * t ≡ (a2 - a1) (mod m2)
rhs = (a2 - a1) // g
m1_unit = m1_reduced % m2_reduced
inv_m1_unit = pow(m1_unit, -1, m2_reduced)
t = (rhs * inv_m1_unit) % m2_reduced
x0 = a1 + m1 * t
M = m1 * m2_reduced
x0 %= M
return x0, M
def even_nums_that_sum_to(k: int, n: int) -> Generator[tuple, Any, None]:
if n == 1:
yield (k,)
else:
for x in range(2, k + 1, 2):
for i in even_nums_that_sum_to(k - x, n - 1):
yield (x,) + i
def find_optimal_parameters():
best = None # (score, N, A, B, C, D, E)
# Using the fact that any optimal solution summing to 256 or less
# cannot be worsened by an additional belt that makes up the difference:
for A, B, C, D in tqdm(even_nums_that_sum_to(256, 4), desc="Combination"):
if D <= 8:
continue
step_e = gcd(A, B, C, D)
for E in range(0, floor(sqrt(D) - 2) ** 2, step_e):
N1, M1 = crt(-E, A, -E, D)
N2, M2 = crt(0, B, 0, C)
if N1 == None or N2 == None or M1 == None or M2 == None:
continue
N, _ = crt(N1, M1, N2, M2)
if N == None:
continue
score = N + E
if best is None or score > best[0]:
best = (score, N, A, B, C, D, E)
return best
def worst_cycle(A, B, C, D):
best = (None, None, None)
N2, M2 = crt(0, B, 0, C)
if N2 == None or M2 == None:
return best
for dA in range(0, A, 2):
for dD in range(0, D, 2):
N1, M1 = crt(-dA, A, -dD, D)
if N1 == None or M1 == None:
continue
N, _ = crt(N1, M1, N2, M2)
if N == None:
continue
if best[0] == None or best[0] < N:
best = (N, dA, dD)
return best
def main():
result = find_optimal_parameters()
if result is None:
print("No feasible solution found under given constraints.")
return
score, N, A, B, C, D, E = result
print(f"Maximized N + E = {score}")
print(f"A={A}, B={B}, C={C}, D={D}, E={E}")
print(f"N={N}")
score, dA, dD = worst_cycle(A, B, C, D)
if score is None:
print("No worst solution found under given constraints.")
return
print(f"Worst starting positions:")
print(f"dA={dA}, dD={dD}")
print(f"N={score}")
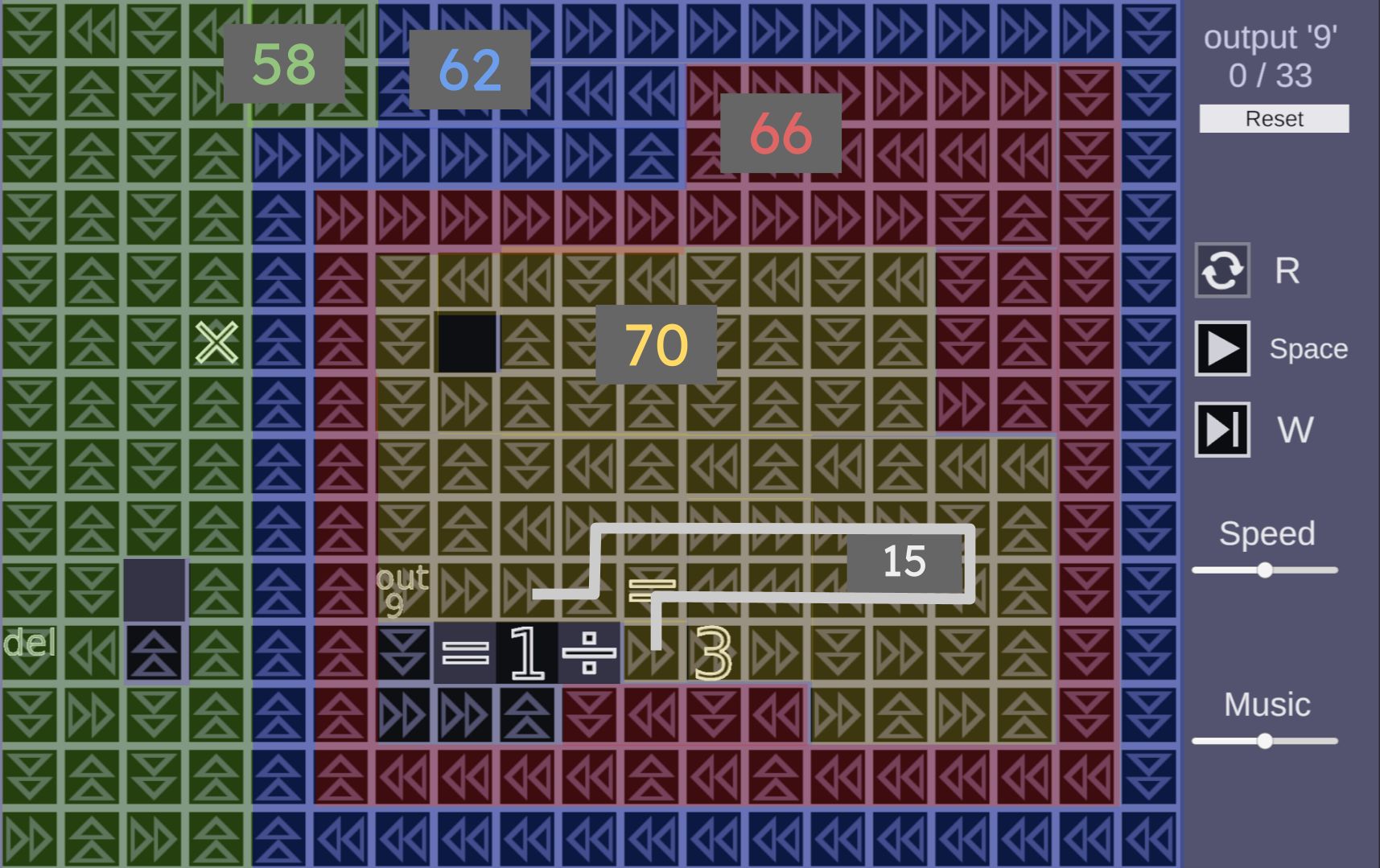
If our one-loop machine took 16615 cycles to complete, how many will this modulo monster take?

My computer spent three weeks "rendering" this picture.
Can we do worse?
Well, this is an example of a configuration that shoves five loops into the playable area.
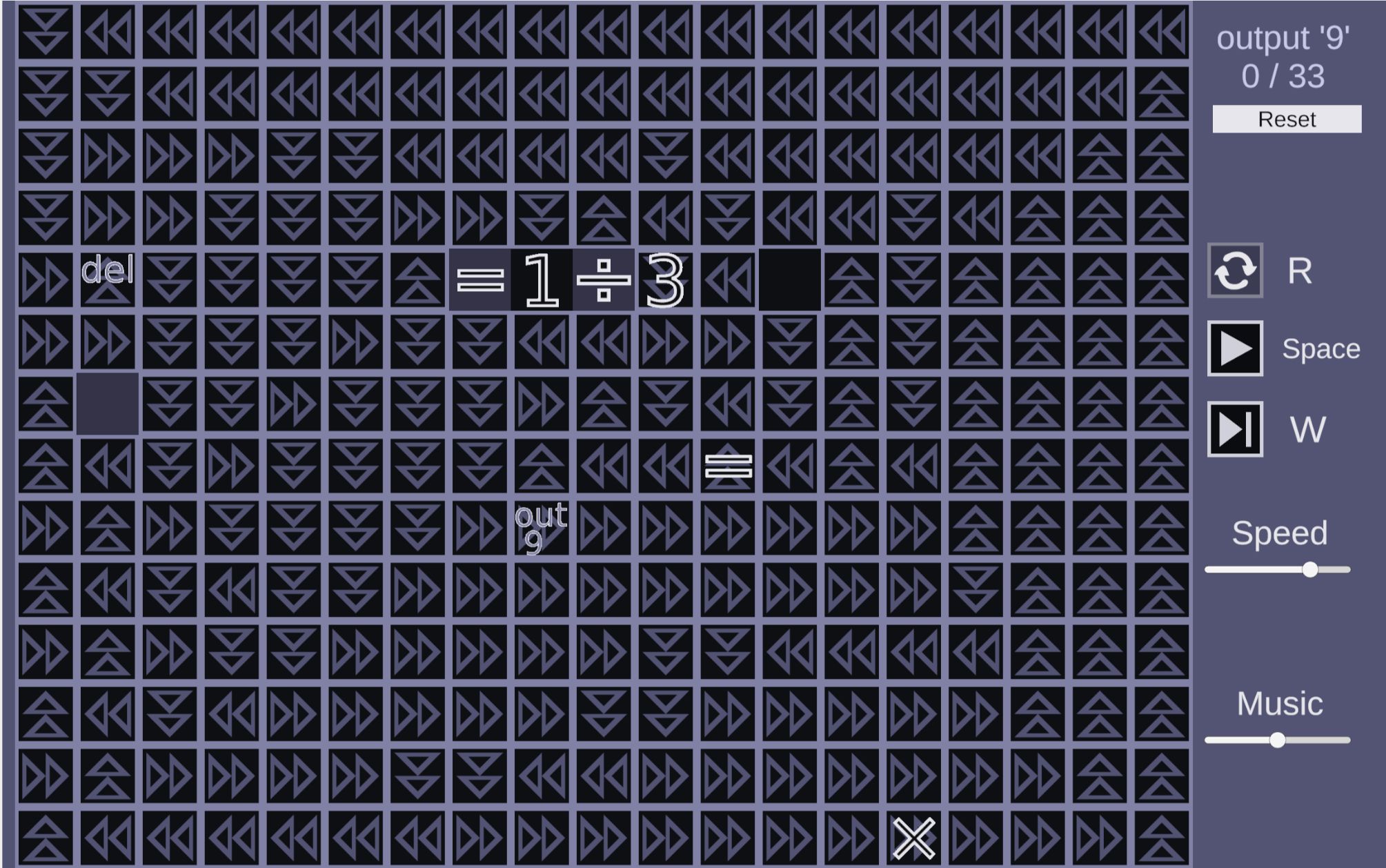
It's hard to make sure that there's only one point where five loops are allowed to line up.
Whether or not that configuration is the worst possible five-loop configuration is an open question right now!
I'll report back in a month or two or six, depending on whether or not I decide to verify the five-loop machine I settle on as part of the report.
bcat112a
bcat112a is someone I look up to very much. Their puzzle games advance the boundaries of both solvable puzzles and programmable puzzles simultaneously, and they truly never miss, so to speak.
If you haven't checked out Squishcraft, put it on your weekend todo list. It's great! And bonkers difficult!
Along with Jack Lance and Phistomefel, bcat112a probably influenced my future in a substantial way. Solving world-class puzzles is a pure delight, but setting them has got to be on another level yet.
So, down the setter's path I go!
Here's the first step in this journey of a thousand miles

